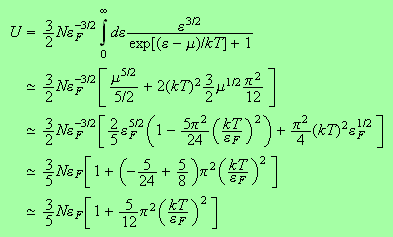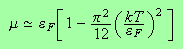
In the lectures I quoted, without proof, the results
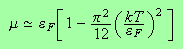
and
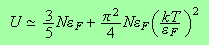
which are good for low enough values of
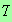 .
Here is the derivation (and I only recommend the following for those who are
particularly good at maths).
.
Here is the derivation (and I only recommend the following for those who are
particularly good at maths).
To get the chemical potential we use
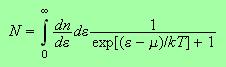
with
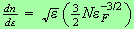 and to get the internal energy we have a similar integral, just an extra
factor of
and to get the internal energy we have a similar integral, just an extra
factor of
 in the numerator.
in the numerator.
Therefore we have to perform integrals of the type
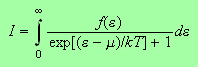
where
 for
for
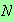 and
and
 for
for
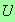 .
.
It must be possible to write

You can see that this must be possible because at
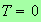 the denominator of the integrand is equal to unity for
the denominator of the integrand is equal to unity for
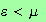 and
infinite for
and
infinite for
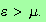 Let's try and manipulate our integral into this form.
Let's try and manipulate our integral into this form.
Put
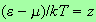 .
Then we have
.
Then we have
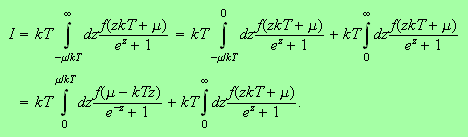
Now use a neat trick and write
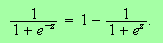
This leads to
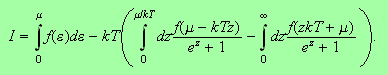
Now we notice that the middle of these three integrals has an upper limit
which we can safely set to infinity. You can see this because as
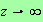 the integrand is approximately equal to
the integrand is approximately equal to
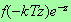 .
Since
.
Since
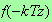 is only powerlike in
is only powerlike in
 ,
it follows that the contribution to the integral from the large
,
it follows that the contribution to the integral from the large
 region is suppressed exponentially, i.e. by a factor
region is suppressed exponentially, i.e. by a factor
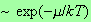 .
Such a term will be smaller than any power of
.
Such a term will be smaller than any power of
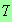 as
as
 .
Therefore we can safely write
.
Therefore we can safely write
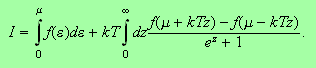
We have succeeded in manipulating the integral into a useful form. The first
term is the term we calculated in the lectures whilst the second term can be
expanded in a Taylor series about
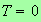 ,
i.e.
,
i.e.
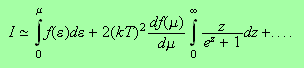
The integral over
 gives
gives
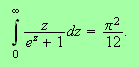
We can now go ahead and determine the chemical potential and the internal energy.
For the chemical potential
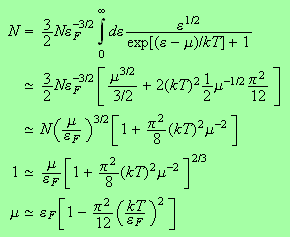
and for the internal energy